Формализация качественных знаний
При формализации качественных знаний может быть использована теория нечетких множеств [Заде, 1974], особенно те ее аспекты, которые связаны с лингенетической неопределенностью, наиболее часто возникающей при работе с экспертами на естественном языке. Под лингвистической неопределенностью подразумевается не полиморфизм слов естественного языка, который может быть преодолен на уровне понимания смысла высказываний в рамках байесовской модели [Налимов, 1974], а качественные оценки естественного языка для длины, времени, интенсивности, для целей логического вывода, принятия решений, планирования.
Лингвистическая неопределенность в системах представления знаний задается с помощью лингвистических моделей основанных на теории лингвистических переменных и теории приближенных рассуждении [Kikerf 1978]. Эти теории опираются на понятие нечеткого множества, систему операций над нечеткими множествами и методы построения функций принадлежности.
Одним из основных понятий, используемых в лингвистических моделях, является понятие лингвистической переменной. Значениями лингвистических переменных являются не числа, а слова или предложения некоторого искусственного либо естественного языка. Например, числовая переменная "возраст" принимает дискретные значения между нулем и сотней, а целое число является значением переменной. Лингвистическая переменная "возраст" может принимать значения: молодой, старый, довольно старый, очень молодой и т. д. Эти термы-лингвистические значения переменной. На это множество (как и на числа) также налагаются ограничения. Множество допустимых значений лингвистической переменной называется терм-множеством.
При вводе в ЭВМ информации о лингвистических переменных и терм-множестве ее необходимо представить в форме, пригодной для работы на ЭВМ. Лингвистическая переменная задается набором из пяти компонентов: <Л, Т(А), U, <7, Af>, где Л-имя лингвистической переменной; Г (Л)-ее терм-множество;
U- область, на которой определены значения лингвистической переменной; 6 описывает операции по порождению производных значений лингвистической переменной на основе тех значений, которые входят в терм-множество.
С помощью правил из О можно расширить число значений лингвистической переменной, т. е. расширить ее терм-множество. Каждому значению а лингвистической переменной Л соответствует нечеткое множество Ха, являющееся подмножеством V. По аналогии с формальными системами правила из G часто называют синтаксическими Наконец, компонент М образует набор семантических правил. С их помощью происходит отображение значений лингвистической переменной а в нечеткие множества Ха и выполняются обратные преобразования. Именно эти правила обеспечивают формализацию качественных утверждений экспертов при формировании проблемной области в памяти ИС.
На рис. 2Л показаны все компоненты, определяющие лингвистическую переменную <возраста>. В качестве терм-множества использовано множество, состоящее из трех значений: очень молодой (Ом), пожилой (п) и старый (с), задаваемых функциями принадлежности на области V, которую называют носителем лингвистических значений. В примере область V-года жизни от 0 до 150 лет, В качестве семантических правил выступают отображения, задаваемые функциями принадлежности 0<Цд(")<1 к нечетким множествам Лои" Хи, Хе. Как видно из рис. 2Л. человек, возраст которого равен 60 годам, принадлежит
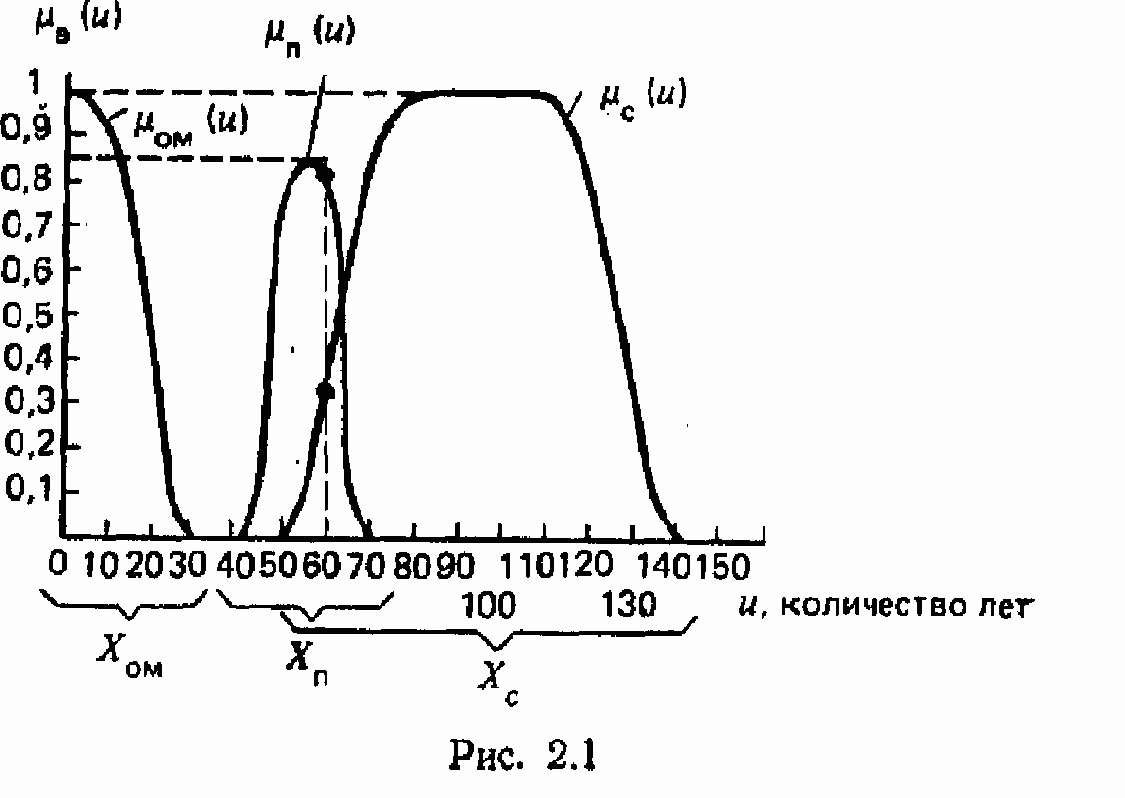
к Хоы со значением 0 (т. в, человек в 60 лет не является очень молодым), к Ха со значением 0.8 и к Хс со значением 0.4.
Для перехода от качественных описаний к формализованным необходимо построить отображения, входящие в М, т. е. построить функции принадлежности, В таком виде подобная задача была исследована в [Блишун, 1987]
При получении от экспертов информации о виде функций принадлежности необходимо учитывать характер измерений (первичные и производные измерения) и тип шкалы, на которую проецируются измерения и на которой будут определяться функции принадлежности [Глотов и др.. 1976]. На этой шкале задается вид допустимых операторов и операций, т. е. некоторая алгебра для функций принадлежности. Кроме того, следует различать характеристики, которые можно измерять непосредственно и характеристики, которые являются качественными и требуют попарного сравнения объектов, обладающих этими характеристиками" чтобы определить их отношение к исследуемому понятию.
Можно выделить две группы методов построения функций принадлежности: прямые и косвенные. В прямых методах эксперт непосредственно задает правила определения значений функции принадлежности lia(u). Эти значения согласуются с его предпочтениями на множестве объектов следующим образом: для любых Ki, и 2 s U имеет место Ио(УО<Ио(и2) тогда и только тогда, когда йд предпочтительнее и\, т. е, в большей степени определяется понятием а; для любых уь u^eU имеет место Ца(1)=Ца(2) тогда и только тогда, когда Нч и и не различаются по отношению к понятию а. К прямым методам относится непосредственное задание функции принадлежности таблицей, формулой или примером [Zadeh, 1975; Ragade et aL, 1977; Thoie et a.. 1979].
В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворялись заранее сформулированные условия. Экспертная информация является только исходной для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки. Примерами дополнительных условий могут служить следующие: функция принадлежности должна отражать близость к заранее выделенному эталону, объекты множества являются точками в параметрическом пространстве [Scala, 1978]; результатом процедуры обработки должна быть функция принадлежности, удовлетворяющая условиям интервальной шкалы [Жуковин и др.. 1983]; при попарном сравнении объектов, если один объект оценивается в k раз сильнее, чем другой то второй объект оценивается в \/k раз сильнее, чем первый объект [Saaty, 1974]. и т. д.
Как правило, прямые методы используются для описания понятий, которые характеризуются измеримыми признаками (высотой, ростом, массой, объемом).
В этом случае удобно непосредственное задание функции принадлежности. К прямым методам можно отнести методы, основанные на вероятностной трактовке функций принадлежности: а(и)==Р(а/и), т, е. вероятность того, что объект ueU будет принадлежать к множеству, которое характеризует понятием Так как люди часто искажают оценки, например сдвигают их в направлении концов оценочной шкалы [Thole et al., 1979].то прямые измерения, основанные на непосредственном определении значений функции принадлежности, могут быть использованы только в том случае, когда такие искажения незначительны или маловероятны. Косвенные методы более трудоемки, чем прямые, но обладают стойкостью к искажениям в ответе. Результатом применения косвенных методов является интервальная шкала. В [Thole et al.. 1979] выдвигается для косвенных методов "условие безоговорочного экстремума": при определении степени принадлежности множество исследуемых объектов должно содержать по крайней мере два объекта, численные представления которых на интервале [0. 1] - О и 1 соответственно.
Функции принадлежности могут отражать мнение как некоторой группы экспертов, так и одного уникального эксперта. Комбинируя возможные дэа метода построения функций принадлежности с двумя типами экспертов (коллек-тивным и уникальным), можно получить четыре типа экспертизы [Блишун, 1988]